Перайсці да зместу

Тэорыя гравітацыі Лесажа

З Вікіпедыі, свабоднай энцыклапедыі

У 1690 годзе швейцарскі матэматык [1] Нікола Фаціа дэ Дзюілье і ў 1756 Жорж-Луі Ле Саж у Жэневе прапанавалі простую кінетычную тэорыю гравітацыі, якая дала механічнае тлумачэнне ураўненні сілы Ньютана. [2] З-за таго, што праца Фаціа не была шырока вядомая і заставалася неапублікаванай доўгі час, менавіта апісанне тэорыі Ле Сажам стала тэмай падвышанай цікавасці ў канцы XIX стагоддзя, калі дадзеная тэорыя была вывучана ў кантэксце толькі што адкрытай кінетычнай тэорыі газаў. [3] Гэта механічнае тлумачэнне гравітацыі ніколі не атрымлівала шырокага прызнання і да пачатку XX стагоддзя тэорыя ў цэлым лічыцца аспрэчанай, у асноўным з-за праблем, узнятых Максвелам [4], Пуанкарэ. [5]Акрамя таго, у другім дзесяцігоддзі XX стагоддзя Альберт Эйнштэйн стварыў агульную тэорыю адноснасці, праўда, прызнанне да яе прыйшло некалькі пазней. Хоць тэорыя Ле Сажа ўсё яшчэ вывучаецца некаторымі даследчыкамі, яна не разглядаецца асноўнай навуковай супольнасцю як жыццяздольная тэорыя.

Асноўная тэорыя

[правіць | правіць зыходнік]
P1: Адно цела
Няма чыстай накіраванай сілы

Тэорыя сцвярджае, што сіла гравітацыі - гэта вынік руху маленькіх часціц, якія рухаюцца на высокай хуткасці ва ўсіх напрамках ў Сусвеце. Інтэнсіўнасць патоку часціц мяркуецца аднолькавай ва ўсіх напрамках, такім чынам, ізаляваны аб'ект A удараецца часціцамі з усіх бакоў, у выніку чаго ён падвяргаецца ціску ўнутр аб'екта, але не падвяргаецца накіраванай сіле P1.

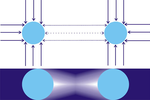
P2: Два цела "прыцягваюць" адно другое

Аднак, у выпадку прысутнасці другога аб'екта B, частка часціц, якія інакш бы ўдарылі па аб'екце A з боку B, перахопліваецца, такім чынам B працуе як экран, г.зн. з напрамку В аб'ект A ударыць менш часціц, чым з процілеглага кірунку. Аналагічна, аб'ект B будзе ўдараны меншай колькасцю часціц з боку A, у параўнанні з процілеглым бокам. Гэта значыць, можна сказаць, што аб'екты A і B «экрануюць» адзін аднаго, і абодва цела прыціскаюцца адно да аднаго выніковым дысбалансам сіл (P2). Такім чынам, ўяўнае прыцягненне паміж целамі ў дадзенай тэорыі на самай справе з'яўляецца паменшаным ціскам на цела з боку іншых цел. Па гэтай прычыне дадзеную тэорыю часам называюць «push гравітацыя» або «ценявая гравітацыя», хоць найбольш часта сустракаецца назва «гравітацыя Лесажа».

Прырода сутыкненняў

[правіць | правіць зыходнік]
P3: Процілеглыя патокі

Калі сутыкненне цела A і гравітацыйнай часціцы цалкам пругкае, інтэнсіўнасць адлюстраваных часціц будзе настолькі ж моцнай, як і тых часціц, што прыходзяць, г.зн. чыстая накіраваная сіла не паўстане. Дадзенае сцвярджэнне дакладна і ў тым выпадку, калі мы ўвядзем другое цела У, якое будзе дзейнічаць як экран для гравітацыйных часціц у кірунку цела A. Гравітацыйная часціца C, якая ў звычайнай сітуацыі ўдарыла б па аб'екце A, блакуецца У, але іншая часціца D, якая ў звычайнай сітуацыі не ўдарыла б па A, перанакіроўваецца пругкім адлюстраваннем на аб'ект B, і такім чынам замяняе C. Такім чынам, калі сутыкненне цалкам пругкае, адлюстраваныя часціцы паміж аб'ектамі A і B цалкам кампенсуюць любы «экрануе» эфект. Каб растлумачыць сутнасць гравітацыйнай сілы, мы павінны выказаць здагадку, што сутыкненне часціц не з'яўляецца цалкам пругкім, ці хаця б тое, што адлюстраваныя часціцы запавольваюцца, г.зн. іх імпульс памяншаецца пасля сутыкнення. Гэта прывядзе да таго што ад аб'екта А адыходзіць струмень з паменшаным імпульсам, але прыходзіць струмень з нязмененным імпульсам, такім чынам з'яўляецца чысты накіраваны імпульс да цэнтра аб'екта A (P3). Калі прыняць гэтую здагадку, то адлюстраваныя часціцы ў выпадку 2 цел, якія ўзаемадзейнічаюць, цалкам не кампенсуюць эфект экранавання, з-за таго, што адлюстраваны паток слабей, чым струмень, які падае на цела.

Зваротна-квадратычная залежнасць

[правіць | правіць зыходнік]
>P4: ХЗваротно-квадратычная залежнасць

З нашай здагадкі, што некаторыя (ці агульныя) гравітацыйныя часціцы, якія сыходзіліся на аб'екце, абсарбуюцца або запавольваюцца дадзеным аб'ектам, вынікае, што інтэнсіўнасць патоку гравітацыйных часціц, выпусканага ад масіўнага аб'екта, менш, чым інтэнсіўнасць патоку, які падае на дадзены аб'ект. Можна выказаць здагадку, што гэты дысбаланс імпульсу патоку і адпаведна сілы прыкладзенай на любое цела паблізу аб'екта, размеркаваны па сферычнай паверхні з цэнтрам на дадзеным аб'екце (P4). Дысбаланс імпульсу патоку над усёй сферычнай паверхняй навакол аб'екту не залежыць ад памеру навакольнага сферы, у той жа час плошча паверхні сферы павялічваецца прапарцыйна квадрату радыусу. Такім чынам, дысбаланс імпульсу на адзінку плошчы памяншаецца ў зваротна-квадратычнай залежнасці ад адлегласці.

Прапарцыянальнасць масе

[правіць | правіць зыходнік]

З фактаў, паказаных вышэй, узнікае сіла, якая прама прапарцыянальная толькі паверхні цела. Але сіла гравітацыі прапарцыйная таксама масе. Каб задаволіць неабходнасць у прапарцыянальнасці ад масы, тэорыя сцвярджае, што: а) базавыя элементы матэрыі вельмі малыя, такім чынам, матэрыя ў асноўным складаецца з пустой прасторы; б) што гравітацыйныя часціцы настолькі малыя, што толькі вельмі малая частка з іх перахопліваецца матэрыяй. У выніку чаго, «цень» кожнага цела прама прапарцыянальная паверхні кожнага з базавых элементаў матэрыі. Калі зараз выказаць здагадку, што элементарныя непразрыстыя (для гравітацыйных часціц) элементы ўсёй матэрыі ідэнтычныя (г.зн. маюць такое ж стаўленне шчыльнасці да паверхні), то з гэтага вынікае, што экрануючы эфект (хоць бы прыблізна) прапарцыянальны масе (P5).

P5: Пранікальнасць, згасанне і прапарцыянальнасць масе

Ранняе развіццё тэорыі

[правіць | правіць зыходнік]

Фаціа

[правіць | правіць зыходнік]

Фаціа прадставіў першую фармулёўку сваіх думак аб гравітацыі ў лісце да Гюйгенса вясной 1690.[1] Праз два дні ён зачытаў змест пісьма перад Лонданскім Каралеўскім таварыствам. У наступныя гады Фаціа напісаў некалькі чарнавых рукапісаў сваёй галоўнай працы «De la Cause de la Pesanteur». Некаторыя фрагменты гэтых рукапісаў былі ў наступным набыты Ле Сажам (гл. ніжэй) і былі знойдзеныя раскіданымі сярод папер Ле Сажа ў 1944 годзе. На падставе гэтых фрагментаў і канспекта, зробленага самім Фаціа, Бернар Ганьебэн паспрабаваў аднавіць працы Фаціа. [6] Ганьебэн не ведаў, што поўная копія аднаго з ранніх чарнавікоў, напісаных у 1701 годзе, была знойдзена Карлам Бопам ў 1915 годзе сярод папер сям'і Бернулі і легла ў аснову выдання працы Фаціа, апублікаванага Бопам ў 1929 годзе. [7] Выданне Бопа больш падрабязнае, чым выданне Ганьебэна, але выданне Ганьебэна ўключае ў сябе выпраўлення зробленыя Фаціа да 1743 ўключна, на 40 гадоў пазней стварэння чарнавіка, на якім грунтуецца выданне Бопа. Для дэталёвага аналізу працы Фаціа і параўнаннем паміж выданнямі Бопа і Ганьебэна - глядзіце публікацыі Цэхе.[8] Ніжэй прыведзенае апісанне ў асноўным заснаванае на выданні Бопа. Яны былі названыя Фаціа «Праблемы I-IV», у той жа час паміж Праблемай I і праблемай II фармулюецца 5 тэарэм. Праблемы II-IV складаюць другую палову выдання Бопа і ўтрымліваюць матэматычна найбольш перадавыя ідэі тэорыі Фаціа, але яны не былі ўключаныя Ганьебэнам ў яго выданне прац Фаціа.

Некаторыя уласцівасці тэорыі Фаціа

[правіць | правіць зыходнік]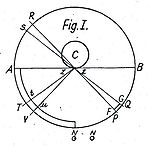
Р6: Піраміда Фаціа

Піраміда Фаціа (Праблема I): [9] Фаціа выказаў здагадку, што сусвет напоўнены драбнюткімі карпускуламі, якія рухаюцца з вельмі высокай хуткасцю бязладна і прамалінейна ва ўсіх напрамках. Каб праілюстраваць свае думкі, ён выкарыстаў наступны прыклад: уявіце аб'ект С, на якім размешчана бясконца маленькая плоскасць zz і намаляваная сфера з цэнтрам у zz. У гэтую сферу Фаціа змясціў піраміду PzzQ, у якой некаторыя карпускулы рухаюцца ў напрамку zz, а таксама некаторыя карпускулы, якія ўжо былі адлюстраваны аб'ектам C і, такім чынам, пакідаюць плоскасць zz. Фаціа выказаў здагадку, што сярэдняя хуткасць адлюстраваных часціц менш і такім чынам імпульс слабей, чым у падальных на цела карпускул. У выніку атрымліваецца адзін паток, які штурхае ўсё цела па кірунку да zz. Такім чынам, з аднаго боку хуткасць патоку застаецца сталай, але з іншага боку пры большай блізкасці да zz шчыльнасць патоку павялічваецца і такім чынам яго інтэнсіўнасць прапарцыянальная 1⁄r2. А так як можна намаляваць бясконцую колькасць такіх пірамід вакол C, прапарцыянальнасць 1⁄r2 можна застасаваць да ўсёй вобласці вакол C.

Паменшаная хуткасць: каб пацвердзіць здагадку, што карпускулы пасля адлюстравання рухаюцца з паменшанымі хуткасцямі, Фаціа зрабіў наступныя здагадкі: [10] a) звычайнае рэчыва або гравітацыйныя карпускулы, або і тое і іншае - няпругкія; b) сутыкнення цалкам пругкія, але карпускулы не абсалютна цвёрдыя, і такім чынам пераходзяць у стан ваганняў пасля сутыкнення і (або) c) з-за трэння карпускулы пачынаюць круціцца пасля сутыкнення. Гэтыя ўрыўкі тэорыі Фаціа - найбольш малазразумелыя, таму што ён ніколі дакладна не вырашыў, які з варыянтаў сутыкненняў найбольш пераважны.[11] Аднак, у апошняй версіі сваёй тэорыі у 1742 годзе ён скараціў звязаныя ўрыўкі і напісаў "поўная пругкасць або пругкая сіла" для карпускул і «няпоўная пругкасць» для звычайнага рэчывы, такім чынам карпускулы павінны быць адлюстраваны з паменшанымі хуткасцямі.[12] <br / У дапаўненне, Фаціа сутыкнуўся з іншай праблемай: што адбываецца, калі карпускулы сутыкаюцца адна з адной? Няпругкае сутыкненне прыводзіць да пастаяннага памяншэння хуткасці карпускул і такім чынам да памяншэння гравітацыйнай сілы. Каб пазбегнуць гэтай праблемы, Фаціа выказаў здагадку, што дыяметр карпускул вельмі малы ў параўнанні з адлегласцю паміж імі, такім чынам, узаемадзеяння паміж карпускул адбываюцца вельмі рэдка.

Кандэнсацыя: [13] каб змякчыць супярэчнасці, якія ўзніклі з-за таго, што чым менш хуткасць карпускул, тым больш карпускул будзе акумулявацца каля цел, Фаціа выказаў здагадку, што карпускулы адлюстроўваюцца ў піраміду TzzV. У той жа час, калі карпускулы прыходзяць з боку PQ дасягаюць C, то адлюстраваныя часціцы не дасягаюць TV, а прыбываюць у tu. Аднак, гэта не прыводзіць да бясконцага назапашвання часціц, а толькі да кандэнсацыі, бо павялічаная шчыльнасць застаецца сталай. Фаціа звярнуў увагу на тое, што, працягваючы павялічваць хуткасць, Tt можа стаць колькі заўгодна малым па адносінах да TZ.

P7: Мадэль рэчывы з крышталічнай рашоткай (двадцаціграннік)

Сітаватасць звычайнага рэчывы: [14] каб забяспечыць прапарцыянальнасць масе, Фаціа выказаў здагадку, што звычайнае рэчыва надзвычай пранікаямае для гравітацыйнай вадкасці (патоку карпускул). Ён зрабіў накіды 3 мадэляў, каб пацвердзіць сваё меркаванне. a) Фаціа выказаў здагадку, што матэрыя складаецца з маленькіх «шарыкаў», дыяметр якіх у параўнанні з адлегласцю паміж імі «бясконца» малы. Але ён адкінуў дадзенае меркаванне, на падставе таго, што пры такіх умовах «шарыкі» будуць імкнуцца адзін да аднаго, і цела не будзе заставацца «стабільным». b) Пасля гэтага ён зрабіў здагадку, што «шарыкі» могуць быць злучаныя лініямі або прутамі, і фармуюць ў некаторым родзе крышталічную рашотку. Аднак ён прызнаў непрыдатнай і гэтую мадэль таксама. Калі некаторыя атамы знаходзяцца побач адзін з адным, то гравітацыйная вадкасць не зможа прабрацца ў гэтую структуру аднолькава з усіх бакоў, і адпаведна прапарцыянальнасць масе немагчымая. c) У рэшце рэшт, Фатио прыбраў і «шарыкі», пакінуўшы толькі лініі або сетку, зрабіўшы лініі «бясконца» меншымі ў параўнанні з адлегласцю паміж імі, дасягнуўшы такім чынам максімальнай праніклівай здольнасці.

Сіла ціску корпускул (Праблема II):[15] Ужо ў 1690 годзе Фаціа выказаў здагадку, што «штурхальная сіла», якая выклікаецца карпускуламі на роўнай плоскасці, у 6 разоў менш, чым сіла, якая была б створана гэтымі ж карпускуламі, калі б яны былі размешчаны па нармалі да паверхні. Фаціа прыводзіць доказ сваёй здагадкі, шляхам вызначэння сілы, якая выклікаецца карпускуламі на пэўным пункце плоскасці zz. Ён выводзіць формулу p = ρv²zz/ 6. Гэтае рашэнне вельмі падобна на формулу вядомую ў кінетычнай тэорыі газаў p=ρv²/3, якая была знойдзена Даніілам Бернулі ў 1738 годзе. Гэта першы раз, калі назіраецца блізкая аналогія паміж такім выглядам гравітацыйных тэорый і кінетычнай тэорыяй газаў - задоўга да развіцця базавых канцэпцый больш позняй з тэорый. Аднак значэнне, атрыманае Бернулі, у 2 разы больш, чым значэнне Фаціа, таму што (па Цэхе) Фаціа разлічыў толькі значэнне mv для змены імпульсу пасля сутыкнення, а не 2mv і, такім чынам, атрымаў няправільны вынік (яго вынік верны толькі для цалкам няпругкіх сутыкнення). Фаціа спрабаваў выкарыстаць сваё рашэнне не толькі для тлумачэння гравітацыі, але таксама і для тлумачэння паводзін газаў. Ён паспрабаваў сканструяваць тэрмометр, які павінен быў паказваць «стан руху» малекул паветра і, такім чынам, падлічваць тэмпературу. Але Фаціа (у адрозненне ад Бернулі) не ідэнтыфікаваў цеплыню з рухам часціц паветра, ён выкарыстаў іншую вадкасць, якая павінна быць адказная за гэты эфект.[16] Таксама не вядома, аказалі ці працы Фаціа ўплыў на Бернулі ці не.

Бясконцасць (Праблема III): [17] У гэтай чале Фаціа даследуе сувязь паміж паняццем «бясконцасць» і яе стаўленнем да сваёй тэорыі. Фаціа часта тлумачыў свае здагадкі тым фактам, што розныя з'явы «бясконцыя менш або бясконцыя больш» чым іншыя, і такім чынам шматлікія праблемы могуць быць зменшаны да нявызначанага значэння. Напрыклад, дыяметр «пераборак» «бясконца менш», чым адлегласць паміж імі ці што хуткасць карпускул «бясконца больш», чым у звычайнага рэчывы або розніца ў хуткасці паміж адлюстраванымі або няадлюстраванымі карпускуламі «бясконца маленькая".

Супраціўлене асяроддзя (Праблема IV): [18] Гэта матэматычна самая складаная частка тэорыі Фаціа. Тут ён спрабуе ацаніць супраціўленне патоку карпускул целу, якое рухаецца. Выкажам здагадку, што u - хуткасць звычайнага рэчывы, v - хуткасць гравітацыйных часціц і ρ - шчыльнасць асяроддзя. У выпадку, калі v << u і ρ = const, Фаціа зрабіў выснову, што супраціўленне роўна ρu2. У выпадку, калі v >> u і ρ = const, супраціўленне роўнае 4/3ρuv. У гэтым месцы Ньютан канстатаваў, што адсутнасць супраціўлення арбітальным рухам планет патрабуе надзвычайнай разрэджанасці любога асяроддзя ў космасе. Таму Фаціа паменшыў шчыльнасць асяроддзя і заявіў, што каб захаваць дастатковую гравітацыйную сілу, гэта памяншэнне павінна быць кампенсавана змяненнем v «зваротна прапарцыйнае квадратнаму кораню шчыльнасці». Гэта вынікае з карпускулярнаму ціску Фаціа, які прапарцыянаотны ρv2. Згодна з Цэхе, ідэя Фаціа павялічыць v да вельмі вялікіх значэнняў сапраўды зробіць супраціўленне вельмі маленькім у параўнанні з гравітацыяй (і наогул калі заўгодна маленькім) з-за таго, што супраціўленне у мадэлі Фаціа прапарцыйны ρuv, а гравітацыя (г.зн. ціск кврпускул) прапарцыйны ρv2.

Зноскі

  1. ↑ а б Fatio, 1690a
  2. ↑ Le Sage, 1756
  3. ↑ Thomson, W. 1873
  4. ↑ Maxwell і 1875
  5. ↑ Poincaré, 1908
  6. ↑ Fatio, 1743
  7. ↑ Fatio, 1701
  8. ↑ Zehe, 1980
  9. ↑ Fatio, 1690a; Fatio, 1701, pp. 32-35; Zehe, 1980, pp. 134-156
  10. ↑ Fatio, 1690a; Fatio, 1701, p. 34;
  11. ↑ Zehe, 1980, pp. 198-204.
  12. ↑ Zehe, 1980, p. 385; Fatio, 1743, pp. 134-135.
  13. ↑ Fatio, 1690a, p. 387; Fatio, 1690c, pp. 38-39;
  14. ↑ Fatio, 1701, pp. 36-38 and 59-61; Zehe, 1980, pp. 206-214.
  15. ↑ Fatio, 1701, pp. 47-49; Zehe, 1980, pp. 227-241 and 198-205
  16. ↑ Zehe, 1980, p. 239
  17. ↑ Fatio, 1701, pp. 49-50; Zehe, 1980, pp. 242-254.
  18. ↑ Fatio, 1701, pp. 50-64. Zehe, 1980, pp. 255-276.

Гл. таксама

[правіць | правіць зыходнік]
Узята з "https://be.wikipedia.org/wiki/Тэорыя_гравітацыі_Лесажа"